

En géodésie, elle exprime également léloignement dun point par rapport au géoïde. Since we know that the three triangles formed by the altitude are all similar, we can.
DEFINITON OF ALTITUDE GEOMETRY PLUS
Then the reflections of over, , and are on the circumcircle of : L altitude (du latin : altitudo) est historiquement une notion géographique qui désigne la hauteur géométrique verticale entre un point et un référent altimétrique, le plus souvent le niveau de la mer. A triangles hypotenuse A to B is split by altitude C to D. Let be a triangle and its orthocenter.If the orthocenter's triangle is acute, then the orthocenter is in the triangle if the triangle is right, then it is on the vertex opposite the hypotenuse and if it is obtuse, then the orthocenter is outside the triangle.The orthocenter and the circumcenter of a triangle are isogonal conjugates.Note that so the altitude of is the perpendicular bisector of Since the circumcenter exists, the orthocenter must too. Let the line through parallel to and the line through parallel to intersect at Define similarly. That seems somewhat overkill to prove the existence of the orthocenter. The line containing these three points is known as the Euler line of the triangle, and also contains the triangle's de Longchamps point and nine-point center. This proof also gives us the result that the orthocenter, centroid, and circumcenter are collinear, in that order, and in the proportions described above. It follows that is parallel to and is therefore perpendicular to i.e., it is the altitude from. Then the triangles, are similar by side-angle-side similarity. Let be the point such that is between and and. So it's okay to have an altitude that is not inside your triangle.Note: The orthocenter's existence is a trivial consequence of the trigonometric version Ceva's Theorem however, the following proof, due to Leonhard Euler, is much more clever, illuminating and insightful.Ĭonsider a triangle with circumcenter and centroid. If I look at the other two altitudes in this obtuse triangles, we're going to have one altitude going like that I'm going to have to extend that side as well and we'll drop down another altitude. Notice that I had to extend that opposite side. So if we pick this vertex, our opposite sides are over here but that opposite side doesn't continue to where this altitude will drop. Median A median of a triangle is a line segment from a vertex of the triangle to the midpoint of the side opposite that vertex. So a third case is the obtuse triangle, and here is where I say to a line containing the opposite side. However if I pick my 90 degree angle as my vertex, then we'll be able to see that altitude inside the triangle. This line containing the opposite side is called the extended base of the altitude. forming a right angle with) a line containing the base (the opposite side of the triangle). In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to (i.e. If I pick this vertex right here the altitude will just be that leg of the triangle. An altitude is the perpendicular segment from a vertex to its opposite side. That's going to be that leg of the triangle.
DEFINITON OF ALTITUDE GEOMETRY FULL
2 View Full Answer altitude of a triangle is the height of the triangle 0 altitude is the line segment which. If we look at a right triangle over here we can see that if I pick this vertex right here, we already have an altitude drawn. In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e. Notice that all three altitudes are inside the triangle. We would have two more altitudes, each of which would go perpendicular to the opposite side. So if I were to pick this top vertex right here, the altitude would go straight down perpendicular to the opposite side. So if we look at an acute triangle, there are going to be three altitudes, one form each vertex. In each triangle, there are three triangle. It's not always to the opposite side and you're going to see why in a second here. Altitudes are defined as perpendicular line segments from the vertex to the line containing the opposite side. So this definition is written very carefully. What we're talking about is a perpendicular segment, remember this symbol right here means perpendicular-I'm trying to get you used to seeing these symbols-from a vertex to a line containing the opposite side.
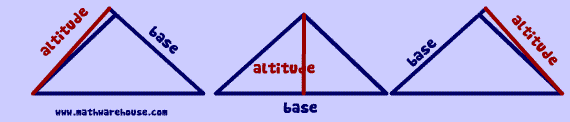
When we're talking about triangles, there's a special segment three in each triangle called an "Altitude." So we're not talking about skiing here.


 0 kommentar(er)
0 kommentar(er)
